
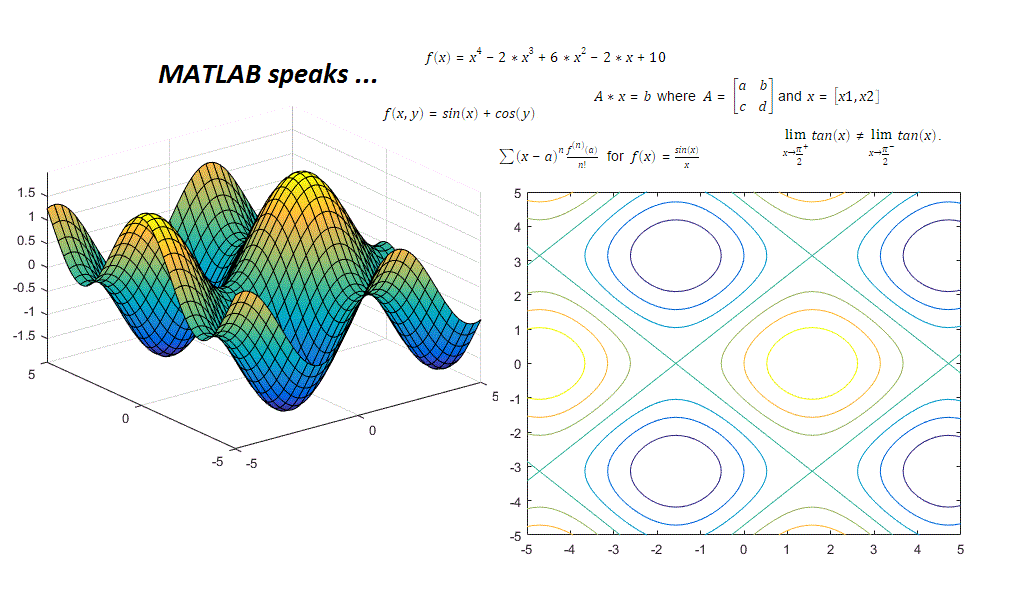
However, most languages cannot do this with matrices, so, instead, we multiply both sides of the equation by the inverse of the coefficient matrix A: In fact, with MATLAB we can use the divided into operator to do this. If we were working with scalars, we would divide both sides of the equation by A. To do this, we need to isolate x on one side of the equation. Once the system of equations has been written in matrix form, what we want is to solve the equation Ax = b for the unknowns x. MATLAB itself provides capabilities to define a matrix as well as to execute the related linear algebra computations.Ī x = b a 11 a 12 a 13 ⋯ a 1 n a 21 a 22 a 23 ⋯ a 2 n a 31 a 32 a 33 ⋯ a 3 n ⋮ ⋮ ⋮ ⋮ ⋮ a m 1 a m 2 a m 3 ⋯ a m n x 1 x 2 x 3 ⋮ x n = b 1 b 2 b 3 ⋮ b m In particular, the user does not need to provide first-and second-order derivatives for the objective function and the constraints. SymNumOpt is relatively easy to use since it embeds TOMLAB syntax and functionality. al., 2005), can be employed to solve the problem. The reformulated optimization problem can have multiple local optimal solutions and thus a combination of a stochastic global solver, e.g., multiMin and multiMINLP for purely continuous and (mixed-)integer problem, respectively (Holmström et. The numeric computation capability is facilitated by TOMLAB ( Holmström, 1999) and the associated optimization solvers. MuPAD / Symbolic Math Toolbox ( Sorgatz and Wehmeier, 1999) provides the symbolic computation capability. The proposed computational implementation, called SymNumOpt, unifies the symbolic-numeric computations into an integrated framework. Wicaksono, Wolfgang Marquardt, in Computer Aided Chemical Engineering, 2013 4 Computational Implementation Investigate the poly function, which finds the characteristic equation for a matrix, and the polyeig function, which solves a polynomial eigenvalue problem of a specified degree.ĭanan S. Investigate some of the other numerical integration functions, such as integral, integral2 for double integrals, and integral3 for triple integrals. In the Command Window, type “odeexamples” to see some ODE example codes. Investigate the Ordinary Differential Equation (ODE) solve functions, such as ode23 and ode45, which use the Runge-Kutta integration methods. Investigate the norm function to find a vector or matrix norm. Investigate the functions that return eigenvalues and eigenvectors, such as eig and eigs. Investigate the blkdiag function, which will create a block diagonal matrix. Investigate linear algebra functions, such as rank for the rank of a matrix, or null, which returns the null space of a matrix. Investigate the fzero function, which attempts to find a zero of a function near a specified x value.

Investigate the fminsearch function, which finds local minima for a function. Investigate the interp1 function, which does a table look-up to interpolate or extrapolate. Investigate passing matrices to the set functions, using the ‘rows’ specifier. Investigate the use of ‘R2012a’ to see future changes to the set functions versus the use of ‘legacy’ to preserve the previous values.

Investigate the index vectors returned by the set functions. Investigate the flag introduced in R2015a to omit NaN in functions such as max, min median, etc. Investigate the moving statistical functions introduced in R2016a movmean, movsum, etc. Investigate filtering data, for example using the filter function. Investigate the corrcoef function, which returns correlation coefficients. Perform polynomial multiplication and simplify the results, show that ( x - 1 ) ( x + 1 ) ( x 2 + x + 1 ) ( x 2 + 1 ) ( x 2 - x + 1 ) ( x 4 - x 2 + 1 ) simplifies to x 1 2 - 1.Ω 1 / ( s 2 + ω 1 2 ) ∓ ω 2 / ( s 2 + ω 2 2 ) Most mathematical expressions can be represented in different, but mathematically equivalent forms and the Symbolic Math Toolbox supports a number of operations, including factoring or expanding expressions, combining terms, rewriting or rearranging expressions, and simplification based on assumptions. The Symbolic Math Toolbox supports the Formula Manipulation and Simplification of mathematical functions.


 0 kommentar(er)
0 kommentar(er)
